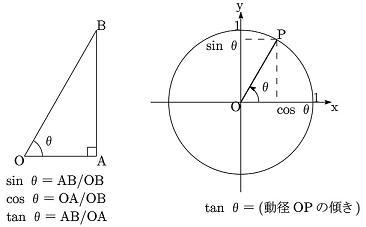
(左の定義は右の定義に含まれる)
| sin(サイン)、cos(コサイン)、tan(タンジェント)という言葉でおなじみの三角関数ですが、 高校では1年で三角比、さらに理科系の2年で三角関数を習います。 本校では1年で三角関数を習います。 三角関数の定義は右の図の通りです。 |  (左の定義は右の定義に含まれる)
|
|
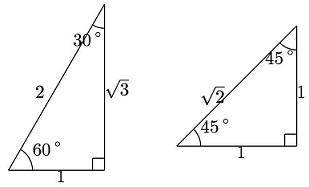
そのとき、特別な角の三角関数の値として
を学びます。 |
|
この問題を考えるとき、三角関数で習った公式
| 二倍角の公式 | cos 2x=2cos2x-1、 |
| 三倍角の公式 | cos 3x=4cos3x-3cos x |
ことがいえます。これを道具にして調べていきます。
| [1] cos 45°=√2/2 であるから、 45°の動径と
x軸、y軸、原点に関して対称な動径が表す角の cos である
cos (45×(2n-1))°(n は自然数)は有理数でありません。 奇数は必ず 2n-1 と表されるので、 (*)より A が奇数なら cos A°は有理数でないことがわかります。 | 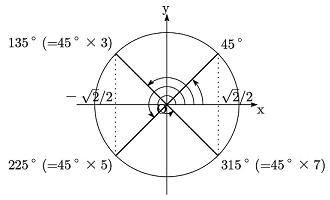
|
| [2] cos 30°=√3 /2 であるから、cos 30°は有理数ではありません。 また、30°の動径とx軸、y軸、原点に関して対称な動径が表す角の cos である cos (30×(6n±1))°(n は自然数)も有理数でありません。 30×(6n±1)=2×3×5×(6n±1) と分解できるので、 (*)より A=2×(6n±1)=12n±2 の型の偶数に対する cos A°も有理数ではありません。 | 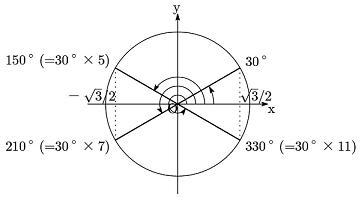
|
| [3] 右の図から cos 72°=((√5)-1)/4 であることがわかります。 したがって、72°の動径とx軸に関して対称な動径が表す角の cos である cos (72×(5n±1))°(n は自然数)は有理数ではありません。 72×(5n±1)=23×32×(5n±1) と分解できるので、 (*)よりまず、A=2×(5n±1)=10n±2 の型の偶数に対する cos A°も有理数ではありません。 [4] また、(*)より A=4×(5n±1)=20n±4 の型の偶数に対する cos A°も有理数ではありません。 [5] さらに、(*)より A=6×(5n±1)=30n±6 の型の偶数に対する cos A°も有理数ではありません。 | 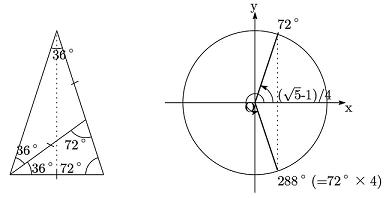
|
[6] 残った A は20、40、60、80の4個です。
cos 80°=x とおくと三倍角の公式より
cos 240°=4x3-3x=-1/2 を満たします。
x が既約分数 x=m/n で表されたと仮定します。 これを代入して整理すると
2m(4m2-3n2)=-n3 となります。
左辺から n は偶数(n=2k と表される)であり、仮定より
m は奇数です。 再び代入して 2m(4m2-12k2)=-8k3 すなわち
m(m2-3k2)=-k3 となります。
いま、k が奇数とすると、右辺は奇数ですが、
左辺は奇数×偶数で偶数となり矛盾です。 そこで、k が偶数とすると、
m が奇数であることから m2-3k2 は
8で割り切れないといけません。 ところが m2-3k2 は奇数なので矛盾です。
以上により、x=cos 80°は有理数ではないことがいえました。
(*)より、cos 20°、cos 40°も有理数ではありません。
| A | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 | 52 | 54 | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 | 74 | 76 | 78 | 80 | 82 | 84 | 86 | 88 |
| [2]で除外 | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | ||||||||||||||||||||||||||||
| [3]で除外 | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | ||||||||||||||||||||||||||
| [4]で除外 | × | × | × | × | × | × | × | × | × | |||||||||||||||||||||||||||||||||||
| [5]で除外 | × | × | × | × | × | × | ||||||||||||||||||||||||||||||||||||||
| [6]で除外 | × | × | × |
ゆえに
クライマックスシリーズのアドバンテージってどれくらい有利なの? (10. 4.22)
1人を選ぶのに何回じゃんけんしたらよいの? (06. 4.17)
三 角形の固定された内点を通って二等分する直線をひく方法 (03. 5. 2)
選択肢の問題・・・なんで1つも当たらないの? (01. 7.26)